[자료구조] 이진탐색트리

28 Nov 2020

개발

최근 이진탐색트리(BST)에 관련된 내용을 질문 받았다가 내용을 제대로 숙지하지 못하고 있어 답변을 잘해내지 못했던 경험이 있다. 해당 경험을 다시 하지 않기 위해 BST에 대해서 정리해보고 나아가 업그레이드 버전인 레드 블랙 트리까지 알아보도록 하자.

이진탐색트리란?

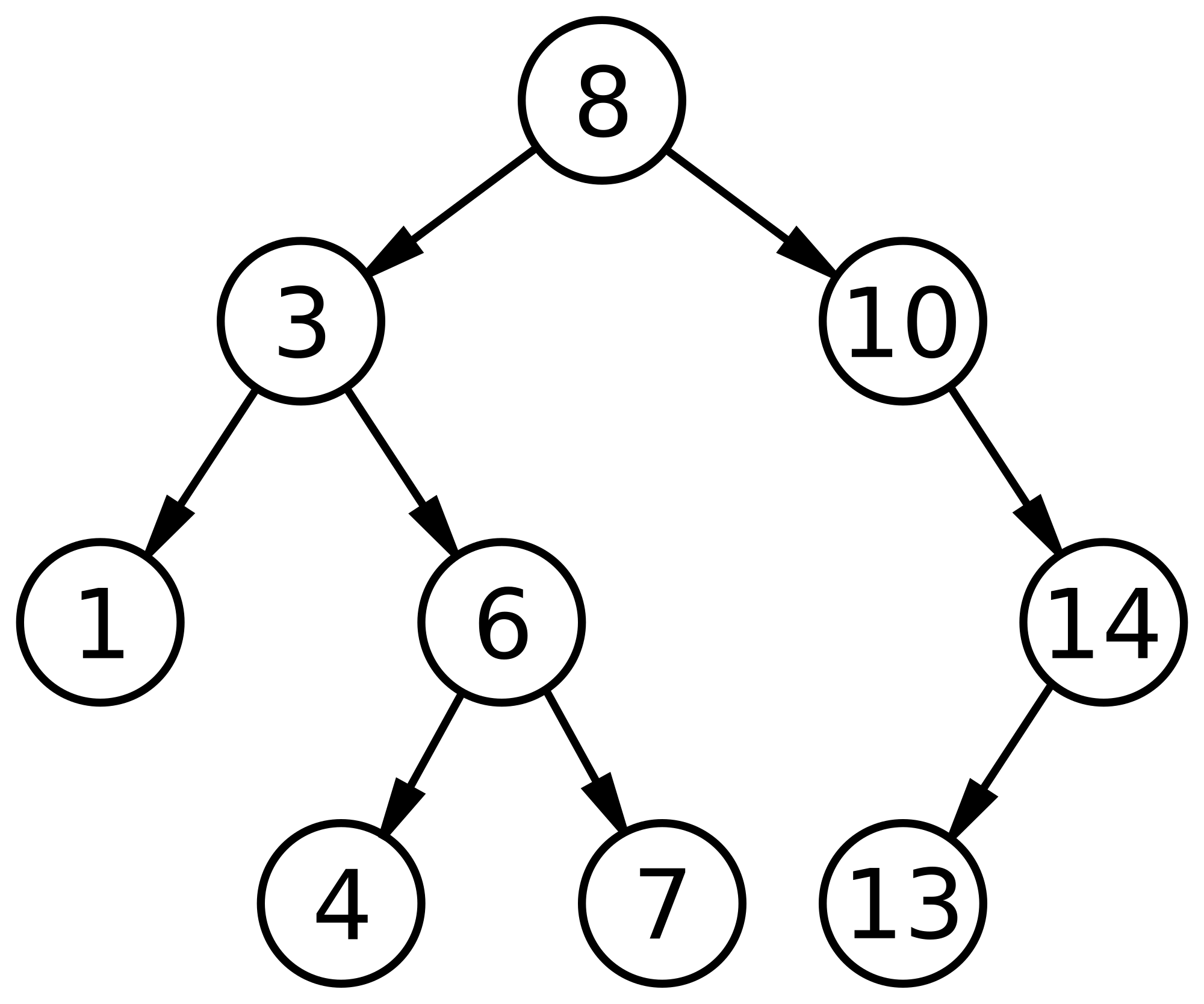
이진탐색트리는 왼쪽 서브 트리의 모든 항목은 루트 노드의 데이터보다 작아야하고 오른쪽 서브 트리의 모든 항목은 루트 노드의 데이터보다 커야 한다는 조건을 만족한 이진 트리이다. 이름에서 알 수 있듯이 이 트리의 주 용도는 검색이다. 어떤 노드가 가질 수 있는 데이터의 종류에 대하여 제한을 두기 때문에, 검색 연산의 최악의 경우 복잡도가 O(logn)이 된다.

이진탐색트리의 주요 연산은 다음과 같다.

이진탐색트리의 항목 찾기, 최소 값 찾기, 최대 값 찾기
이진탐색트리에 새 항목 삽입하기
이진탐색트리로부터 항목 삭제하기
k번째 작은 항목 찾기
이진 검색 트리의 항목 정렬하기 등

주요 사항은 다음과 같다.

루트 데이터가 항상 왼쪽 서브 트리 데이터와 오른쪽 서브 트리 데이터 사이에 있기 때문에 중위 탐색을 수행하면 정렬된 리스트가 만들어진다.
이진탐색트리에 대한 문제를 풀 때 대부분의 경우, 왼쪽 서브 트리를 먼저 처리하고 루트 데이터를 처리한 다음 오른쪽 서브 트리를 처리한다.
어떤 항목을 검색할 때 왼쪽 서브 트리의 데이터가 검색하는 항목보다 작으면 왼쪽 서브 트리의 검색은 생략할 수 있다. 오른쪽 서브 트리에서도 비슷하다. 따라서 일반적인 이진트리보다 검색에 걸리는 시간이 적다.

탐색

왼쪽이나 오른쪽으로 탐색 진행하면서 찾는 노드의 값 있으면 리턴, 없으면 null 리턴

    // 재귀 시간복잡도: 최악의 경우 (BST가 경사 트리일 때) O(n), 공간복잡도: 재귀적 스택 때문에 O(n)
    // 트리가 균형 잡힌 경우 O(logn), 보통 트리 높이에 비례

    Node find(Node root, int data){
    	if(root == null) return null;
    	if(data < root.getData())
    		return find(root.getLeft(), data);
    	else
    		return find(root.getRight(), data);
    	return root;
    }

    // 비재귀 시간복잡도: O(n), 공간복잡도: O(1)
    Node find(Node root, int data){
    	if(root == null) return null;
    	while(root){
    		if(data == root.getData())
    			return root;
    		else if(data > root.getData())
    			root = root.getRight();
    		else root.getLeft();
    	}
    	return null;
    }

삽입

이진탐색트리에 데이터를 삽입하려면 먼저 이 항목의 위치를 찾아야 한다. 위치를 찾는 동안 데이터가 이미 존재한다면 무시하고 나오면 된다. 그렇지 않으면, 탐색한 경로의 마지막 위치에 데이터를 추가한다.

    // 시간복잡도: O(n), 공간복잡도: O(n), 반복적 방법은 O(1)
    Node insert(Node root, int data){
    	if(root == null){
    		root = new Node();
    		if(root == null) {
    			System.out.println("Memory Error"); return;
    		} else {
    			root.setData(data);
    			root.setLeft(null);
    			root.setRight(null);
    		}
    	} else {
    		if(data < root.getData())
    			root.setLeft(insert(root.getLeft(), data));
    		else if(data > root.getData())
    			root.setRight(insert(root.getRight(), data));
    	}
    	return root;
    }

삭제

삭제 연산은 다른 연산에 비해 약간 더 복잡하다. 삭제되는 항목이 잎 노드가 아닐 수도 있기 때문이다. 이 연산에서 역시 먼저 삭제하기 원하는 항목의 위치를 찾아야한다.

경우의 수

삭제할 항목이 리프 노드라면 null을 부모 노드에게 리턴하여 자식 포인터를 null로 만든다.
삭제할 항목이 한 개의 자식 노드를 가진다면 현재 노드의 자식을 부모 노드에게 보내면 된다.

삭제할 항목이 두 개의 자식 노드를 가질 경우 일반적인 전략은 이 노드의 키 값을 왼쪽 서브 트리의 최대 항목과 바꾸고 재귀적으로 그 노드를 삭제하는 것이다. 왼쪽 부속 트리의 최대 항목은 오른쪽 자식을 가질 수 없으므로 두 번째 삭제는 쉽다. 오른쪽 서브 트리의 최소 값과 교체할 수도 있다.

  // 시간복잡도 O(n), 공간복잡도 O(n), 반복적 방법은 O(1)
  Node delete(Node root, int data){
  	Node temp;
  	if(root == null)
  		System.out.println("Element not there in tree");
  	else if(data < root.getData())
  		root.setLeft(delete(root.getLeft(), data));
  	else if(data > root.getData())
  		root.setRight(delete(root.getRight(), data));
  	else {
  		if (root.getLeft() != null && root.getRight() != null){
  			temp = findMax(root.getLeft());
  			root.setData(temp.getData());
  			root.setLeft(delete(root.getLeft(), root.getData()));
  		} else {
  			temp = root;
  			if(root.getLeft() == null)
  				return root.getRight();
  			else if(root.getRight() == null)
  				return root.getLeft();
  		}
  		return root;
  	}
  }

레퍼런스

다양한 예제로 학습하는 데이터구조와 알고리즘 for Java, 나라심하 카루만치

더 알아볼 것

AVL 트리
레드 블랙 트리