Perceptron(퍼셉트론)

1957년 로젠블라트가 고안한 알고리즘이다. 이 알고리즘은 딥러닝의 기원이 되는 알고리즘이다.

퍼셉트론이란

• 다수의 신호를 입력으로 받아 하나의 신호를 출력한다.
• 신호는 흐른다/안 흐른다. (1 또는 0의 두가지 값을 가질 수 있다.)
• 아래 그림에서 각 원을 뉴런 또는 노드라고 부른다.
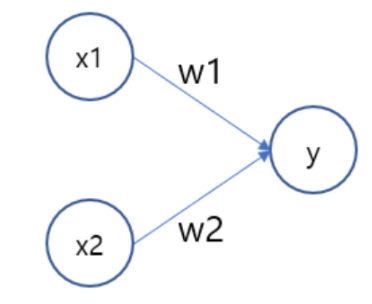
• 입력 신호는 각각 고유한 가중치가 곱해지고 임계값 θ를 넘을때 1로 아니면 0으로 출력 된다. 정리하면 다음과 같은 수식이 된다.
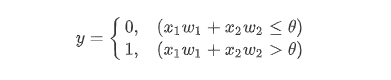
• 가충치의 편항을 도입하면 다음과 같은 수식이 된다.

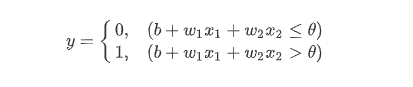
단순 논리 회로

• AND 게이트 | a | b | a & b | | :–: | :–: | :—: | | 0 | 0 | 0 | | 1 | 0 | 0 | | 0 | 1 | 0 | | 1 | 1 | 1 |

• NAND 게이트 | a | b | ~(a & b) | | :–: | :–: | :——: | | 0 | 0 | 0 | | 1 | 0 | 0 | | 0 | 1 | 0 | | 1 | 1 | 1 |

• OR 게이트 | a | b | a & b | | :–: | :–: | :—: | | 0 | 0 | 0 | | 1 | 0 | 0 | | 0 | 1 | 0 | | 1 | 1 | 1 |

• XOR 게이트 | a | b | a b | | :–: | :–: | :———————————————————-: | | 0 | 0 | 0 | | 1 | 0 | 1 | | 0 | 1 | 1 | | 1 | 1 | 0 |

퍼셉트론의 한계

AND, OR, NAND 게이트와 달리 XOR 의 경우 문제가 발생한다. 다음 그림을 통해 알아보자.

• 위의 OR, AND 그래프를 보면 +, - ** 를 하나의 직선으로 분류할 수 있다. 그러나 **XOR과 같은 경우는 하나의 직선으로 분류가 불가능하다.
• 이로 인해 Logistic Regression과 같이 선형 model을 이용해서 해결하는것이 불가능 하다.
• 다층 퍼셉트론(Multi layer perceptron)의 필요성이 대두된다.