Support Vector Machine(SVM)-이론

서포트 벡터 머신은 ML 분야 중 하나로 패턴 인식, 자료 분석을 위한 지도 학습 모델이며 주로 분류와 회귀 분석을 위해 사용한다.

SVM 이란?

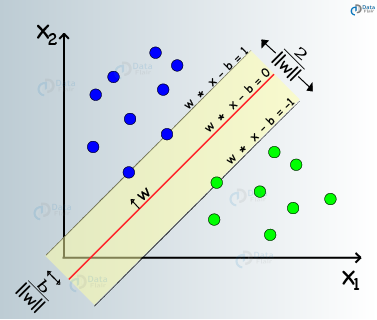
SVM 은 Margin 이라는것을 최대화 하는 training set에 대해서 데이터를 분류하는 최적의 hyperplane 을 찾는다. Margin은 그림상에서 w·x-b=1에서 부터 w·x-b=-1 거리 또는 w·x-b=1 에서 w·x-b=0 까지의 거리를 나타낸다. 밑에서 더 장확하게 정의한다.

Linear SVM

다음과 같이 n개의 training dataset이 주어졌다고 하자.

• Hard-margin : Training Data가 선형 구분 가능할때 DataSet을 구분하고 두개의 평행하는 hyperplane을 거리가 최대가 되도록 선택할 수 있다. 이 두 hyperplane에 의해 bounded인 영역을 margin 이라고 부르고 이 두 hyperplane을에 평행하고 margin을 반으로 나눠주는 hyperplane **을 **maximum-margin hyperplane 이라고 부른다.

  이 hyperplane은 위의 그래프와 같이 나타날 수 있다.

​ 기하적으로 두 hyperplane의 거리는 normal vector의 L2-norm 의 역수의 2배값이다.

​ 따라서

(\vec{x_1}, y_1), ~(\vec{x_2}, y_2),\cdots, (\vec{x_n}, y_n)~~ \text{여기서}~y_i=1 ~또는~0 이고~\vec{x_i}은~n차원~ 벡터이다.\~~ \~~ \

그러면~모든~\text{hyperplane}은~ \vec{w}\cdot\vec{x}-b=0~ \text{꼴로 작성할 수 있다. 여기서 } \vec{w}\text{는 hyperplane의 normal vector이다.}