[머신러닝] Outlier 1
이상치(Outlier) 처리-(1)(Tukey Outlier)
이상치 처리하는데 많이 사용되는 두가지 방법 Tukey Outlier와 Z-Score중 Tukey Outlier에 대해서 알아본다.
이상치(Outlier) 개요
이상치(지대점)는 속성의 값이 일반적인 값보다 편차가 큰 값을 의미한다. 즉, 데이터 전체 패턴에서 동떨어져 있는 관측치를 지칭한다. 이는 평균뿐만 아니라 분산에도 영향을 미치기 때문에 결국은 데이터 전체의 안정성을 저해하게 된다. 그래서 이상치는 반드시 처리해야 하고 검출하는데 있어 많은 시간이 소요되는게 일반적이다.
- 독립변수(x축)에 있는 이상치 : 지대점
- 종속변수(y축)에 있는 이상치 : 아웃라이어
Tukey Outlier
4분위값을 이용해 이상치를 검출하는 방식이다.
제 1 사분위수 - 1.5 * IQR 보다 작거나 제 3사분위수 + 1.5 * IQR 보다 큰 값은 이상치로 판별한다.
사분위수
| 사분위수 | 설명 |
|---|---|
| 제 1 사분위수(Q1) | 데이터의 25%가 이 값보다 작거나 같다. |
| 제 2 사분위수(Q2) | 중위수, 데이터의 50%가 이 값보다 작거나 같다. |
| 제 3 사분위수(Q3) | 데이터의 75%가 이 값보다 작거나 같다. |
| 사분위 범위(IQR) | Q3 - Q1, 데이터의 중간 50%에 대한 범위이다. |
(EX) 7, 9, 16, 36, 39, 45, 45, 46, 48, 51
- Q1 계산 방법
- 공식 : (총도수-1)*0.25+1 의 위치값
- (10-1)*0.25+1 = 3.25 위치 값 = 16+(36-16)*0.25 = 16 + 5 =21
- Q2 = (39 + 45)/2 = 42
- Q3 계산 방법
- 공식 : (총도수-1)*0.75+1 의 위치값
- (10-1)*0.75+1 = 7.75의 위치 값 =45+(46-45)*0.75=45+0.75=45.75
- IQR = 45.75 - 21 = 24.75
## code
import numpy as np
data = np.array([ 7, 9, 16, 36, 39, 45, 45, 46, 48, 51])
## [ 7 9 16 36 39 45 45 46 48 51]
print(np.percentile(data,25)) # 21.0
print(np.percentile(data,50)) # 42.0
print(np.median(data)) # 42.0
print(np,percentile(data,75)) # 45.75
이상치
-
제 1 사분위수 - 1.5 * IQR 보다 작은 수
Q1 -1.5*IQR = 21 -1.5 * 24.75 = -16.125
-
제 3사분위수 + 1.5 * IQR 보다 큰 수
Q3+1.5*IQR = 45.75 + 1.5 * 24.75 = 82.875
## code
IQR = np.percentile(data,75) - np.percentile(data,25)
print(IQR) # 24.75
upper = np.percentile(data,25) - IQR*1.5
print(upper) # -16.125
lower = np.percentile(data,75) + IQR*1.5
print(lower) # 82.875
## 따라서 이상치가 없다.
boxplot 활용
boxplot을 활용해 이사치를 그래프에서 확인해 본다.
import matplotlib.pyplot as plt
plt.boxplot(data)
plt.show()
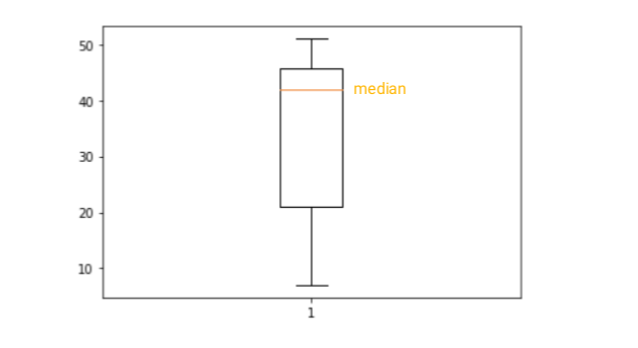
이상치 제거 예제
위의 내용을 가지고 코드를 가지고 다음의 예제를 이용해서
Tukey Outlier를 이용해 이상치를 제거해본다.
## boxplot을 통해 이상치 확인
import numpy as np
import matplotlib.pyplot as plt
data = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 22.1])
fig = plt.figure()
fig1 = fig.add_subplot(1,2,1)
plt.boxplot(data)
plt.show() # 이상치가 존재 한다는것을 알 수 있다.

## outlier 제거
Q1 = np.percentile(data,25) # 4.5
Q3 = np.percentile(data,75) # 11.5
IQR = Q3 - Q1 # 7.0
lower = Q1 - 1.5 * IQR # -6.0
upper = Q3 + 1.5 * IQR # 22.0
data = data[(data>=lower) & (data<=upper)]
fig2 = fig.add_subplot(1,2,2)
plt.boxplot(data)
plt.show()
