구현 코드 링크 : https://github.com/Shinye/TIL/blob/master/DataStructure/hashtable.cpp
” 해시테이블 : 해싱을 통한 검색 - key에 의해 key의 value를 찾음 “
해시의 사전적 의미로는 고기, 야채 등을 잘게 썬다는 뜻을 가지고 있다.
위의 사전적 의미처럼 컴퓨터공학적 관점에서는 큰 데이터를 작은 크기로 바꾸어 주는 의미로 쓰인다. 그래서 주로 암호학, 보안학 관련해서 사용될 땐 패스워드를 해싱 후 저장하는 방법을 쓰기도 한다.
자료구조적 의미의 해싱기법은 크게 해시 함수 / (키와 값을 저장하는) 해시 테이블 두 가지로 구성된다.
여기서 키는 식별자 라고도 불리우며, 다음과 같은 예시로 이해를 할 수 있겠다.
o 전화번호부
키(key) : 이름
값(value) : 전화번호 // 핸드폰 전화번호부 앱에서 이름을 검색하면 전화번호가 나옴
o 사전
키(key) : 단어
값(value) : 단어의 뜻 // 사전 앱에서 단어를 검색하면 단어 뜻이 나옴
이처럼 key를 이용하여 삽입 / 삭제 / 제거 를 할 수 있는데 이를 해싱이라고 부른다.
해시 테이블의 강점은 다음과 같다. (영문 인터넷 강의의 설명이 직관적이라 원문으로 우선 붙여봅니다…)
ARRAY (random access) + LINKED LIST (we want to have our DataStructure be able to grow and shrink.)
Hash tables combine the random access ability of an array with the dynamism of a linked list.
THIS MEANS! (assuming we define our hash table well)
- Insertion can start to tend toward 세타(1) // 세타 : 평균
- Deletion can start to tend toward 세타(1)
- Lookup can start to tend toward 세타(1)
위의 설명대로 원소들의 빠른 접근이 가능한 배열의 장점과, 자료구조의 크기 조정이 자유로운 링크드리스트의 장점이 합쳐진 셈이다. 이 합쳐진 장점들을 토대로, 해시테이블은 삽입, 삭제, 제거 3가지 연산의 평균 검색시간이 O(1) 로 상당히 빠르다는 장점을 가질 수 있다.
하지만 이는 해시테이블을 잘!!! 설계 했을 때의 이야기이다… :-( 최악의 경우 탐색/삽입/제거 시간은 O(n)이다.
따라서 해시테이블을 성공적으로 설계하는 것이 가장 중요한 부분이다.
해시테이블의 구조는 다음과 같다.
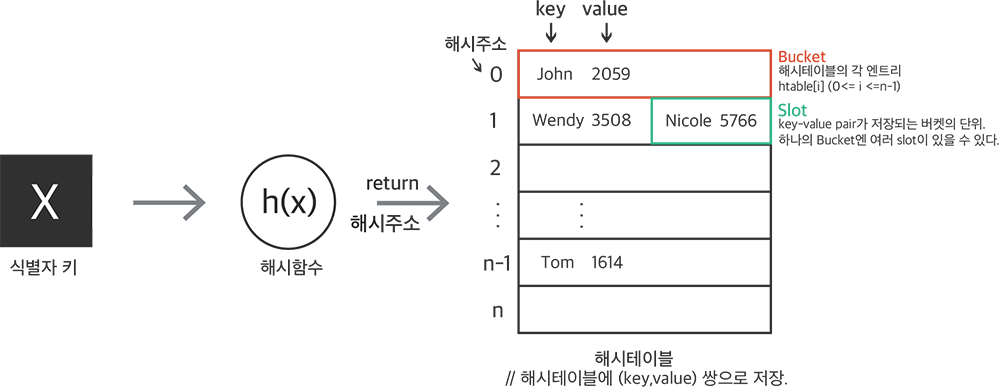
Collision(충돌)
” 서로 다른 key를 가지고 있는데, 해시함수로부터 리턴된 해시주소가 동일한 상황 “
[예시]
크기 365의 1년 365일을 해시테이블이 있다고 가정하자.
한 반의 60명의 학생들의 생일을 각각 테이블에 저장하고자 한다. 60명 학생 모두의 생일이 다르면 해시테이블 안에 값들이 골고루 분포가 되겠지만, 분명 생일이 같은 학생들이 존재한다. 이럴 때 생일이 같은 학생들은 같은 버켓에 값을 넣게 되는데, 이 경우를 '충돌' 이라고 한다.
해시테이블의 Bucket 안에는 여러 개의 slot이 있어 충돌이 생겨도 값을 저장할 수 있긴 하지만, slot의 개수는 유한하기 때문에 주어진 slot이 다 차버리면 분명 저장하지 못하는 상황이 온다. 이러한 충돌이 버킷에 할당된 슬롯 수보다 많이 발생하게 되면 버킷에 더 이상 항목을 저장할 수 없게 되는 오버플로우(overflow) 가 발생 한다.
*동의식별자 : 충돌을 일으킨 서로 다른 식별자
Overflow
” key가 모든 슬롯이 꽉 찬 Bucket에 매핑된 경우 “
앞서 충돌에서 설명하였듯 버킷 안의 슬롯이 모두 찼음에도 불구하고 그 버킷에 key가 할당된 경우를 오버플로우 가 발생했다고 한다. 만약 버켓당 슬롯 수를 1개로 정해놓았으면 충돌과 오버플로우가 동시에 발생한다.
따라서 좋은 해시함수는 해시테이블에 적절히 데이터들을 분산시켜주는 것임을 알 수 있다.
해시함수
해싱기법의 효율성은 해싱함수와 아주 밀접한 관계가 있다. 해시함수는
- 충돌 최소화
- 쉬운 계산
의 조건을 최대한 충족시킬 수 있도록 해야한다.
이상적인 해시함수는 각 버켓 i로 매핑될 확률이 1/m (m == table size)로 같을 경우이다. 이러한 경우를 충족시키면 충돌이 전혀 없는 것이 가능해지고 이를 완전 해시 함수라고 부른다.
…하지만 이건 꿈 같은 일이니^_ㅠ 우리는 충돌과 오버플로우를 방지할 여러 해결책들을 알아갈 필요가 있다.
해시함수는 이미 잘 만들어진 함수를 차용해 쓰는게 좋다. 다행히 좋은 해쉬 함수들이 나와 있으며 Jenkins의 One-at-a-time 해쉬 함수가 대표적인 예라 할 수 있다. 32/64비트 int형의 괜찮은 해쉬 함수를 첨부한다. —> int_hash_func.txt
대표적인 해시함수의 종류는 다음과 같다.
(1) 계산함수 h(k) = k mod M
- 해시 테이블 크기 M 은 주로 소수(prime number)
- 나누기(division) 함수는 실제로 가장 많이 쓰이는 해시 함수로 키 값이 음이 아닌 정수라 가정
- 홈 버킷은 모듈(%) 연산자에 의해 결정됨. 즉, 키 k를 어떤 정해진 임의의 수 D로 나눈 나머지를 홈 버킷으로 사용함 h(k) = k % D
- 버킷 주소의 범위는 0 ~ (D-1) 이고, 해시 테이블에는 적어도 b = D 개의 버킷이 있어야함
** (2) 중간 제곱 함수 **
- 탐색 키를 제곱한 다음, 중간의 몇 비트를 취해서 해시 주소를 생성
- 중간 제곱 함수는 키를 제곱한 후에 그 결과의 중간에 있는 적절한 수의 비트를 취해 홈 버킷을 정함
- 키는 정수라고 가정
- 제곱 수의 중간 비트는 대개 그 키의 모든 비트에 의존하기 때문에 서로 다른 해싱주소를 갖게 될 확률이 높음
(3) 접지 함수
- hash_index = (short) (key ^ (key » 16))
- 이동 폴딩(shift folding)과 경계 폴딩(boundary folding)
- 숫자로 된 키 k를 몇 부분으로 나누면 마지막 부분을 제외하고는 길이가 같아짐
- 나눠진 각 부분들을 더하여 k에 대한 해싱 주소를 만듬
- <shift folding : 이동 폴딩 / 이동 접지> : 마지막을 제외한 모든 부분들을 이동시켜 최하위 비트가 마지막 부분의 자리와 일치하도록 맞춘 뒤, 서로 다른 부분들을 더하여 h(k)를 얻는 방법.
- <boundary folding : 경계 폴딩 / 경계 접지> : 키의 각 부분들을 종이 접듯이 경계에서 겹치게 한 다음, 같은 자리에 위치한 수들을 더하여 h(k)를 얻는 방법.
- 접지 함수 예(skip)
(4) 숫자 분석(digital analysis) 함수
- 키의 각각의 위치에 있는 숫자 중에서 편중되지 않은 수들을 해시 테이블의 크기에 적합한 만큼 조합하여 해시 주소로 사용
- 테이블에 있는 모든 키를 미리 알고 있는 정적(static) file 과 같은 경우에 유용
- 각 키를 어떤 기수(진법) r을 이용해 하나의 숫자로 바꾼 뒤 이 기수를 이용해 각 키의 숫자들을 검사함
- 가장 편향된(skewed) 분산을 가진 숫자를 생략해서 남은 숫자만으로 해서 해시테이블의 주소를 결정 함
Overflow의 처리
-
Chaining
보통 자료구조에서의 Chaining은 연결리스트를 뜻한다고 한다.
- 각 버킷을 연결리스트로 유지 ->
동의식별자들을 동일 버켓에 저장. - 해시 테이블의 htable[i]는 리스트 헤드
- 버킷 안의 각각의 노드들은
slot을 의미.
예시 구조는 다음과 같다.
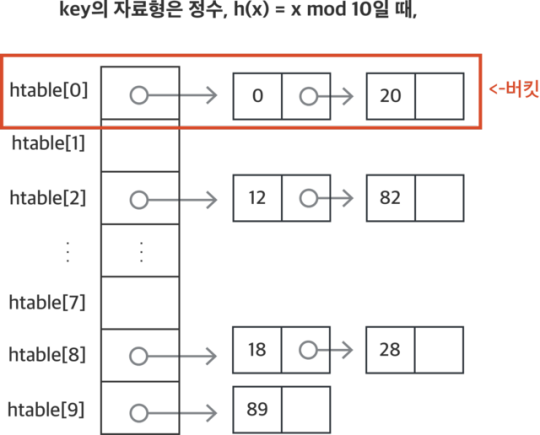
- 각 버킷을 연결리스트로 유지 ->
-
Open Addressing (개방 주소법)
Open addressing 방식은 index에 대한 충돌 처리에 대해서 Linked List와 같은 추가적인 메모리 공간을 사용하지 않고, hash table array의 빈공간을 사용하는 방법으로, Chaining 방식에 비해서 메모리를 덜 사용한다. Open addressing 방식은 크게 세 가지가 존재한다.
1) Linear Probing
Linear Probing 방식은 오버플로우가 발생했을 때, 충돌이 발생한 버킷 뒤에 있는 버킷 중에 빈 버킷을 찾아서 그 곳에 데이터를 넣는 방식이다.
동작 방식의 예는 다음과 같다.
이처럼 오버플로우가 발생 시 순차적으로 탐색하며 비어있는 버켓을 찾을 때까지 계속 진행된다. 최악의 경우, 탐색을 시작한 위치까지 돌아오게 되어 종료(모든 버켓 순회)하게 된다. 캐쉬의 효율은 높으나 데이터의 클러스터링에 가장 취약하며 이 경우 빈 공간을 탐색하기 위한 탐색 시간이 너무 늘어난다는 단점이 있다.
2) Quadratic Probing
2차 함수를 이용해 탐색할 위치를 찾는다. 캐쉬의 효율과 클러스터링에 강하며, linear probing과 double hashing probing의 중간 정도 능력을 가진다.
조정 함수 f()를 이차함수인 f(i) = i^2와 f(i) = -(i^2) 를 번갈아 사용한다.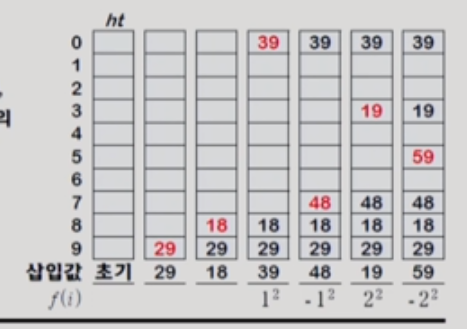
3) Double Hashing
클러스터 방지를 위해, 두 개의 해시 함수를 준비하는 방식. 하나는 최초의 주소를 얻을 때, 그리고 또 다른 하나는 충돌이 일 어났을 때 probing 이동 폭을 얻기 위해 사용.
4) 재해싱
- 해시테이블이 점점 가득 차게 되면 클러스터링으로 인해 연산시간이 길어지는 순간이 온다. => 재해싱이 필요한 순간.
- 원래 해시테이블의 부하 비율(전체 슬롯에서 사용중인 슬롯 비율 : load factor)가 어느 정도 커지면 새로운 해시함수와 2배 이상의
소수 크기의 새로운 해시테이블을 생성한다. 원래 해시테이블의 모든 식별자들을 새로운 해시테이블에 재해싱한다.
탐사 방식에 따라 open-addressing 해쉬의 성능이 달라지지만, 가장 치명적인 영향을 미치는 요소는 바로 해쉬 테이블의 load factor(전체 슬롯에서 사용중인 슬롯 비율. 해시테이블에 들어있는 오브젝트 수를, 버킷 수로 나눈 것.)이다. Load factor가 100%로 증가할수록 데이터를 찾거나 삽입하기 위해 필요한 탐사 횟수는 비약적으로(dramatically) 증가한다. 일단 테이블이 꽉 차게 되면 probing이 실패하여 끝나버리기도 한다. 아래 표는 load factor에 따른 평균 성공 탐색수와 실패수이다.

위 표와 같이 아무리 좋은 해쉬 함수를 쓰더라도 일반적으로 load factor는 80%로 제한된다.(자바에서의 Hashmap은 기본 load factor threshold가 75%이다) 클러스터링에 가장 취약한 linear probing 방식이 load factor가 높을수록 가장 급격하게 성능 저하가 발생하는 것을 확인할 수 있다. 따라서 load factor가 임계점을 넘어 큰 경우의 성능은
double hashing > quadratic > linear 의 순서다.
물론 질 낮은 해쉬 함수는 엄청난 클러스터링을 유발함으로써 아주 낮은 load factor에도 해쉬 테이블의 성능을 상당히 낮아지게 한다. 어떤 문제가 해쉬 함수의 클러스터링을 유발하는지 알기는 쉽지 않아도, 해쉬 함수가 심각한 클러스터링을 유발하게 하는 것은 상당히 쉽다. 그냥 잘 만들어진, 그리고 많은 사람들에 의해 충분히 검증된 공개된 함수들을 가져다 쓰자 :-)
Chaining vs Open Addressing
여기의 설명이 아주 자세하니 여기있는 걸 먼저 읽은 후 다시 보자.
Chaining은 Open Addressing에 비해 다음과 같은 장점을 갖는다.
- 삭제 작업이 간단하다. 삭제 작업이 빈번하다면 open addressing 보다는 chaining 이 낫다.
- chaining 은 클러스터링에 거의 영향을 받지 않아 충돌의 최소화만 고려하면 된다. 반면 open addressing 은 클러스터링까지 피해야 하므로 해쉬함수를 구현하기가 쉽지 않다.
- load factor(전체 슬롯에서 사용중인 슬롯 비율) 가 높아져도 성능 저하가 선형적이다. 아래 그림에서 볼 수 있듯이, open-addressing 방법처럼 급격히 lookup time 이 늘지 않는다. 따라서 테이블 확장을 상당히 늦출 수 있다.

반면 Open Addressing이 Chaining에 비해 가지는 장점은 다음과 같다.
- open-addressing 방식은 테이블에 모두 저장될 수 있고 캐쉬 라인에 적합할 수 있을 정도로 데이터의 크기가 작을수록 성능이 더 좋아진다. 메모리 비용을 아끼려면, 이 방법이 적합하다.
- 반면 테이블의 높은 load factor가 예상되거나, 데이터가 크거나, 데이터의 길이가 가변일 때 chained 해쉬 테이블은 open-addressing 방식보다 적어도 동등하거나 훨씬 더 뛰어난 성능을 보인다. 삭제가 중요하고, 빈번한 연산이라면 chianing 이 더 낫다.
참고 URL
https://www.youtube.com/watch?v=tjtFkT97Xmc
http://core.ewha.ac.kr/publicview/C0101020141210102600802227?vmode=f
http://emzei.tistory.com/128
http://1ambda.github.io/algorithm/design-and-analysis-part1-6/
http://eunpyeonghong.tumblr.com/post/152986466964/%ED%95%B4%EC%8B%9C%ED%85%8C%EC%9D%B4%EB%B8%94hash-table
https://en.wikipedia.org/wiki/Open_addressing
http://bcho.tistory.com/1072
http://egloos.zum.com/sweeper/v/925740
http://d2.naver.com/helloworld/831311
코드 짜는 법
http://www.tutorialspoint.com/data_structures_algorithms/hash_data_structure.htm
http://www.cs.rmit.edu.au/online/blackboard/chapter/05/documents/contribute/chapter/05/linear-probing.html