Lecture3:Linear Regression의 cost 최소화 알고리즘

Simplified hypothesis

기존의 Hypothesis 방정식에는 y절편(+b)의 값이 있지만, 계산의 편의를 위해 실질적인 계산을 할 때는 y절편의 값을 생략한다.

Gradient descent algorithm

직역하자면 경사를 따라 내려가는 알고리즘이라는 뜻을 가진다. 위의 Cost function의 결과 값을 최소화 하기 위해 사용되는 훌륭한 알고리즘이다.
📌 cost 함수의 결과값은 H(x) 값과 가장 근접한 실제 데이터 사이의 차이 값들의 평균이다.

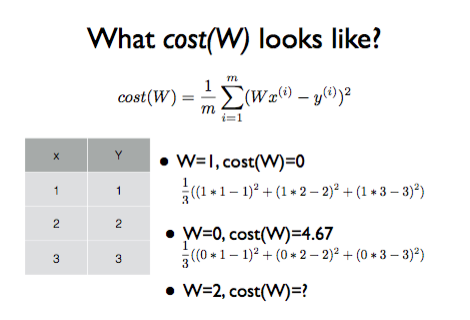
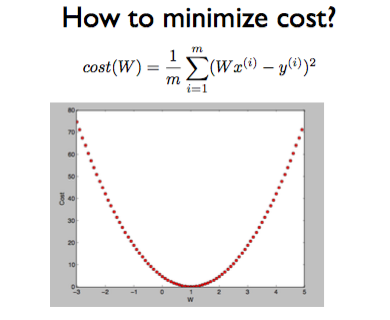
첫 번째 그림의 과정을 촘촘하게 반복한 것의 결과로 두 번째의 그림과 같은 그래프가 생성된다.Cost값이 최소가 되는 지점은 그래프의 최하단 부분일 것이다.
임의의 특정 지점에서부터 더 낮은 cost값을 찾기 위해 경사도를 따라 천천히 내려가다가 경사도가 0에 수렴하는 지점에서 멈춘다.
이 경사도를 알기 위해서는 그래프를 미분 하면 될 것이다. 미분 값이 양수이면 왼쪽으로 조금씩 이동하고, 음수이면 오른쪽으로 조금씩 이동하다 보면 경사도가 0에 수렴하는 값에 도달할 수 있을 것이다.

미분하는 과정(위의 그래프에서 x축인 W값을 조정하는 과정)은 다음과 같이 이루어진다.

참고로 알파 뒤의 분수는 W에 대해서 편미분을 하라는 문법?의미? 이다.
그리고 알파는 Learning Rate 로써 α가 너무 크면 오버슈팅(overshooting)이 될 수 있고, 너무 작으면 최소 비용에 수렴할 때까지 너무 오래 걸리게 된다. 따라서 적당한 값을 넣어주는 것이 좋다.

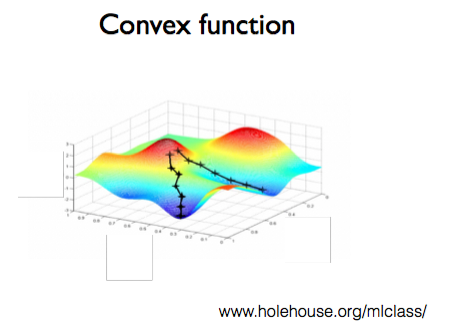
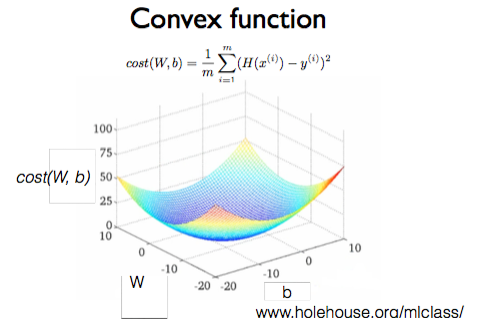
두 장의 그림은 모두 3차원으로 그려져 있고, 가로와 세로는 W와 b, 높이는 cost를 가리킨다. W와 b의 값에 따른 cost를 표현하고 있다. cost를 계산했을 때의 결과를 보여주기 때문에, 쉽게 말해 cost 함수라고 얘기할 수 있다. 오른쪽 그림의 윗부분에 cost 함수의 계산식이 나와 있다.

우리가 만든 모델의 cost 함수가 첫 번째 그래프와 같은 형태로 표현된다면, 어디서 시작하는지에 따라 지역 최저점(local minimum)에 도착할 수도, 도착하지 못할 수 있다. 따라서 Convex(볼록함 이라는 뜻) 함수는 두 번째 그래프와 같이 볼록한 밥그릇 모양을 가져야한다.

참고 URL

04. Linear Regression의 cost 최소화 알고리즘의 원리 설명 (lec 03)