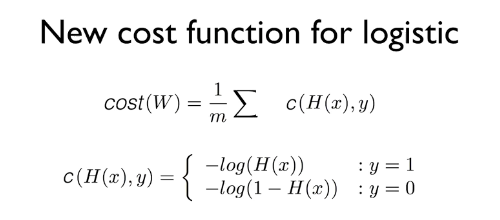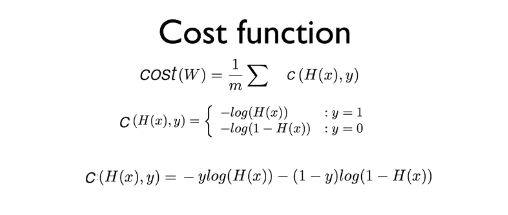Logistic Classification
이전에 다룬 내용은 좌표상에 위치한 데이터를 가로지르는 직선을 그어서 새로운 데이터의 위치를 예측하는 Linear Regression 모델이었다.
이번의 내용은 Linear regression을 활용하여 데이터를 분류하는 모델 이다. 이름은 Logistic Classification 이라고 부른다. 분류에서 가장 단순한 모델로 2가지 중에 하나를 찾는 모델이다.
Logistic classification에는 다음과 같은 예시를 들 수 있다.
일반적으로 찾고자 하는 것을 1로, 그렇지 않은 것을 0으로 둔다.
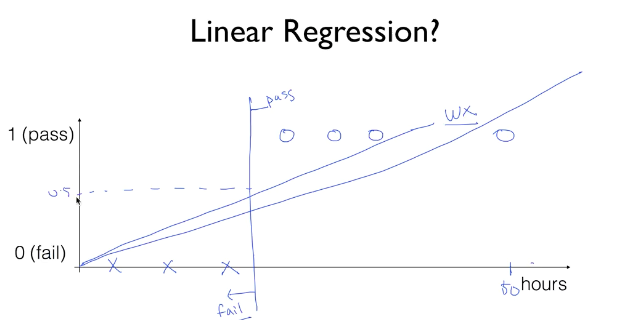
앞서 Linear regression을 활용하여 데이터를 분류한다고 말하였는데, 기존의 Linear regression의 Hypothesis인 Wx+b 를 그대로 활용하면 여러가지 문제점에 마주친다.
위의 그림을 보았을 때, 공부한 시간에 따른 성적(pass/fail)을 표현하고 싶을 때 일정 공부 시간 구간까지는 정해진 Wx+b 직선과 멀지 않은 구간에서 데이터가 속해있다. 하지만 공부한 시간이 상당히 많은 케이스가 발생한다면 위의 그림과 같이 기존의 Wx+b의 예측 범위에서 한참 벗어나게 된다.
이처럼 linear regression을 분류에 바로 사용할 때 발생할 수 있는 문제에 대비하여, 일정 범위보다 크면 1, 작으면 0 과 같은 식으로 0과 1 내에서 답이 나올 수 있도록 추가적인 코드가 필요하다.
그 추가적인 코드를 Sigmoid function 이라고 설명하고 있다.
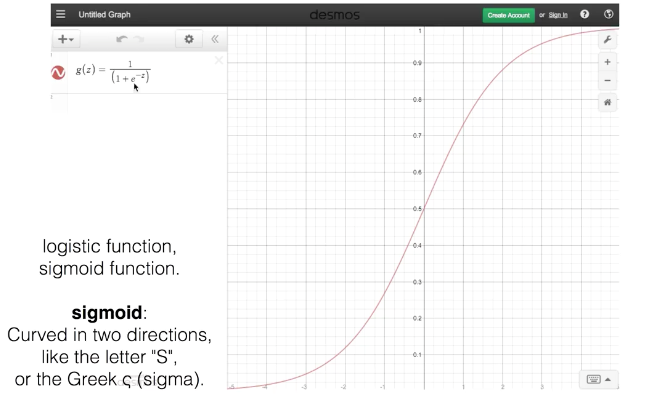
Sigmoid function
Sigmoid는 Linear regression에서 가져온 결과 값(H(X))을 0과 1 사이의 값으로 변환시켜준다. H(X)값이 0일 시엔 0.5로 변환됨.
z = WX+b
sigmoid는 기존의 H(X)=WX+b 가 만들어 내는 결과 값을 0과 1 사이의 값으로 만들어주는 역할을 한다.
정리하자면,
- e로 시작하는 계산식이 0일 때, 1/1이 되어서 최대값인 1이 된다.
- e로 시작하는 계산식이 매우 클 때, (1/큰수)이 되어서 최소값인 0이 된다.
- WX가 0일 때, 지수가 0이 되어, 분모는 2가 되고, 이때 중간값인 1/2이 된다.
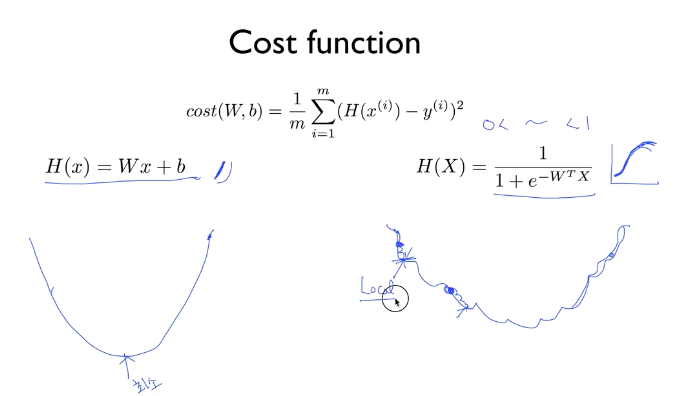
Logistic regression의 Cost 함수
기존의 Linear Regression의 H(X)를 통해 만든 Cost 함수와, sigmoid함수 과정을 더한 Logistic regression의 H(X)를 통해 만든 Cost 함수를 비교한 그림이다.
Logistic regression의 cost함수의 경우는 울퉁불퉁한 모양인데, 기울기 값이 0이 되는 구간이 Linear Regression 처럼 단 하나만 있는 것이 아닌 여러 구간에서 존재한다.
가장 하단에 있는 기울기 0의 지점을 global minimum 이라고 하고, 그 외의 지점에 있는 것은 local minimum 이라고 한다.
따라서 어느 위치에서부터 학습을 시작하느냐에 따라 local minimum에서 학습이 종료되어 잘못된 W,b값을 출력할 수 있다. 따라서 이 cost함수 역시도 수정이 필요하다.
Cost함수의 목적은 비용(예측한 H(X)의 값과 실제 데이터 값 사이의 차이)이 최소가 되는 방향으로 학습하여 올바른 W와 b를 찾는 것이다.
또한 잘못 된 예측을 한 경우 cost 값으로 패널티 값을 최대한 크게 주어(보통 무한대) 보다 확실한 비교가 가능하게 해준다.
다시 말해, 목표로 하는 W와 b를 찾을 수 있다면, 어떤 형태가 됐건 cost 함수라고 부를 수 있다는 뜻이다.
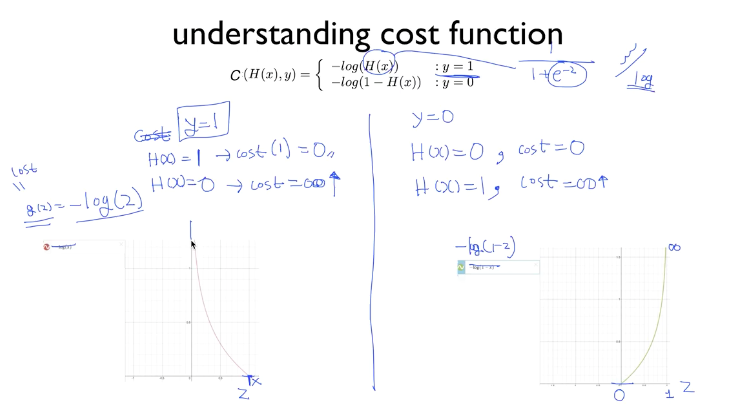
왼쪽은 -log(z)의 그래프이고, 오른쪽은 -log(1-z)의 그래프다.
y(실제 데이터 값) 가 0일 때와 1일 때를 나누어 본다.
-
y가 1일 때
Correct : H(X) = 1일 때는 왼쪽 그래프에서 y는 0이 된다.(cost=0)
Incorrect : H(X) = 0일 때는 왼쪽 그래프에서 y는 무한대(∞)가 된다. (cost=무한대) -
y가 0일 때
Correct : H(X) = 0일 때는 오른쪽 그래프에서 y는 0이 된다. (cost=0)
Incorrect : H(X) = 1일 때는 오른쪽 그래프에서 y는 무한대가 된다. (cost=무한대)
다시 정리하자면,
- y가 1일 때 1을 예측(H(X)=1)했다는 것은 맞았다는 뜻이고, 이때의 비용은 0이다.
- y가 1일 때 0을 예측(H(X)=0)했다는 것은 틀렸다는 뜻이고, 이때의 비용은 무한대이다.
- y가 0일 때 0을 예측(H(X)=0)했다는 것은 맞았다는 뜻이고, 이때의 비용은 0이다.
- y가 0일 때 1을 예측(H(X)=1)했다는 것은 틀렸다는 뜻이고, 이때의 비용은 무한대이다.
맞는 예측을 했을 때의 비용을 0으로 만들어 줌으로써 cost 함수의 역할이 성공적으로 이뤄짐을 알 수 있다.
위의 그림에서 마지막 줄의 공식은 y가 1인 경우와 0인 경우에 따라 달라질 수 있도록 하나로 합쳐 놓은 것이다.
앞에서 만들었던 공식을 cost 함수와 합쳤다. 두 번째 있는 공식은 cost(W)에 대해 미분을 적용해서 W의 다음 번 위치를 계산하는 공식이다.
Linear Regression 알고리즘에서 cost 함수와 gradient descent를 구하는 공식이 각각 있었던 것처럼 Logistic Regression에서도 두 개의 공식이 있어야 하고, 위의 그림에서 확인할 수 있었다.
다만 미분에 대한 공식은 달라졌지만, W를 일정 크기만큼 이동시키는 부분은 여전히 동일하기 때문에 앞서 배운 gradient descent 알고리즘을 여기서도 사용할 수 있고, 텐서플로우를 통해 간단히 구현할 수 있다.
..