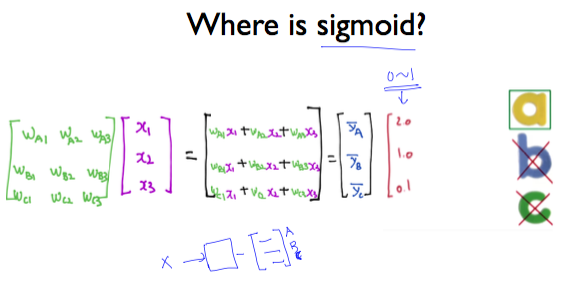Softmax Classification
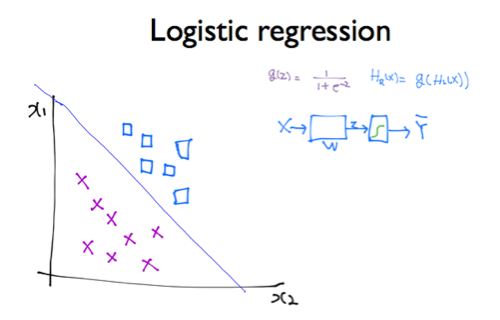
Logistic Regression을 부르는 다른 이름은 binary classification이다.
데이터를 1과 0의 두 가지 그룹으로 나누기 위해 사용하는 모델이다. softmax는 데이터를 2개 이상의 그룹으로 나누기 위해 binary classification을 확장한 모델이다.

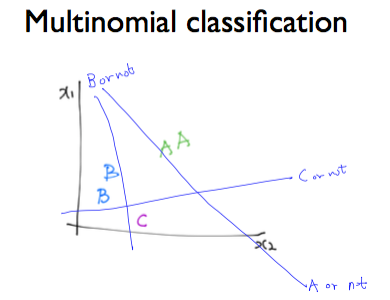
위의 그림과 같이 여러 개의 label(A,B,C) 을 갖는 multinomial classification 경우 다음과 같이 구현할 수 있다. Logistic Regression 처럼 A의 경우/A가 아닌 경우 와 같이 구분한다. (if문과 동일한 원리)
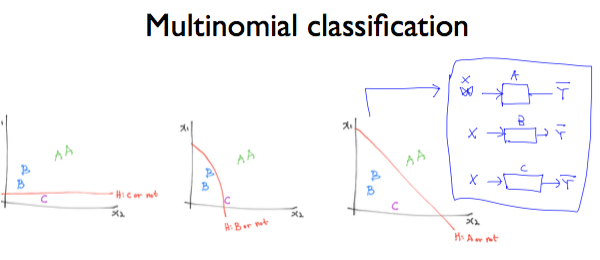
다음과 같이 여러 개의 label로 분류하기 위해서는 여러 개의 binary classification이 필요함을 알 수 있다. 예를들어 학점이 A인경우/B인경우/C인경우 이렇게 각각의 케이스에 따라…
같은 X를 두고 각각 A인지 B인지 C인지 하나씩 classifier에 넣어보는 것이다.
각각의 Binary classification을 구현하려면 이렇게 각각의 행렬을 요구한다. 하지만 행렬을 하나하나 작성하는 것은 번거로우니 아래와 같이 W들을 하나의 행렬로 합친다.
그렇다면 binary classification을 여러 번 적용해서 구한 행렬에 대해 sigmoid 를 적용하는 곳은 어디일까?
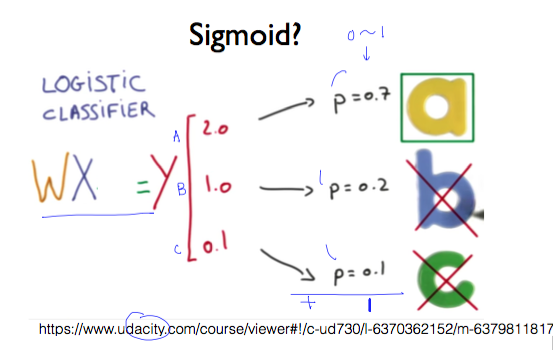
그림 중간에 빨강색으로 표시된 2.0, 1.0, 0.1이 예측된 Y의 값이다. 이것을 Y hat이라고 부른다고 했다. 이 값은 W에 X를 곱하기 때문에 굉장히 크거나 작은 값일 수 있다. 그래서, 이 부분 뒤쪽에 sigmoid가 들어가서 값을 0과 1 사이로 조정하게 된다.
binary classification을 실행한 것이므로 WX 행렬을 곱한 값(Y hat)을 0과 1 사이의 값으로 만들어야 한다.
그림에서 예측한 결과 y가 1개가 아니라 3개라는 점은 중요하다.
선택 가능한 옵션이 a, b, c의 3개가 있어서 binary classification을 3개 사용했고 각각의 결과를 저장해야 하므로 3개가 된다. binary classification을 세 번에 걸쳐 적용하고 있다는 것을 기억하자.
이들 값을 0과 1 사이의 값으로 바꾸니까, 각각 0.7, 0.2, 0.1이 됐다. 이들을 모두 더하면 1이 된다. a, b, c 중에서 하나를 고르라면 a를 선택하게 된다.
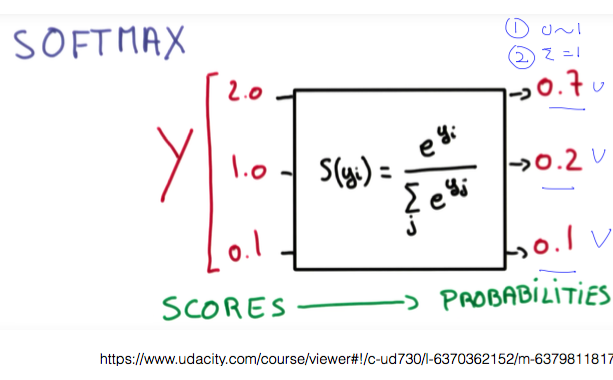
sigmoid 함수의 역할을 해주는 것이 바로 Softmax function 이다.
softmax는 두 가지 역할을 수행한다.
- 입력을 sigmoid와 마찬가지로 0과 1 사이의 값으로 변환한다.
- 변환된 결과에 대한 합계가 1이 되도록 만들어 준다.
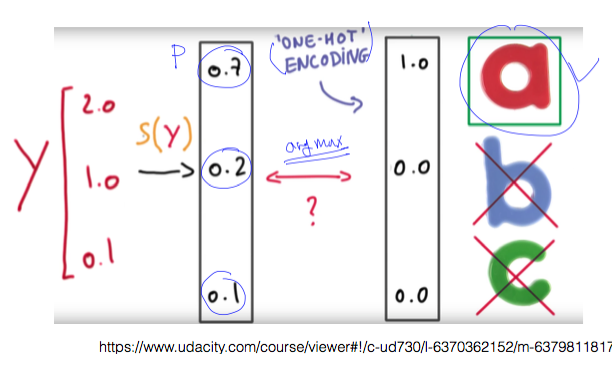
y를 예측한 이후부터의 과정을 알려주는 그림이다.
one-hot encoding은 softmax로 구한 값 중에서 가장 큰 값을 1로, 나머지를 0으로 만든다. 텐서플로우에서는 argmax 함수 라는 이름으로 제공하고 있다.
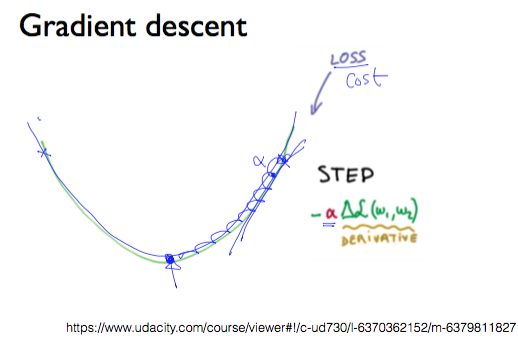
Cost function
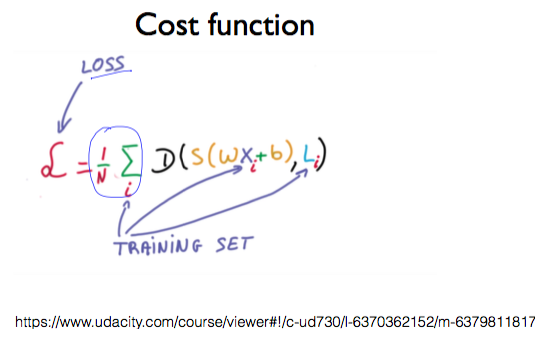
Softmax classification의 Cost function을 구현하면 다음과 같이 작성할 수 있다.
하지만 그 전에 시그마 뒤의 D가 무엇을 의미하는지에 대해 알 필요가 있다.
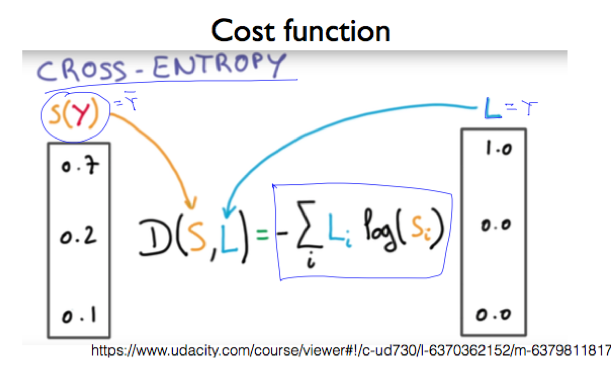
Cross entropy
S(Y)는 softmax가 예측한 값이고, L(Y)는 실제 Y의 값으로 L은 label을 의미한다. cost 함수는 예측한 값과 실제 값의 거리(distance, D)를 계산하는 함수로, 이 값이 줄어드는 방향으로, 즉 entropy가 감소하는 방향으로 진행하다 보면 최저점을 만나게 된다.
그림 오른쪽에 있는 것처럼 1을 전달하면 y는 0이 되고, 0을 전달하면 y는 무한대가 된다. 이때, 비용이 최소로 나오는 것을 선택해야 하므로, 전체 결과가 무한대가 나온다면 선택할 수 없다는 것을 뜻한다.